１５日に四谷例会で行われたレクチャーの続き、第２
回です。
このゲームをプレーするにあたってダブリングキュー
ブの基本的概念を知っておく必要があります。これは、
オッズが関連するゲームを他にプレーしたことがある人
であれば自然と理解できていることだとは思いますが、
ダイスやカードなどによるランダム要素がないゲームし
かプレーされたことがないかたは知らない場合もあると
思います。
バックギャモンに限らず、ダイスなど偶然によるもの
にゲームの結果が大きく影響されるゲームでは、確実に
勝つことはできません。そのため、長い目で見た時の勝
率、予想されうるトータルな結果、いわゆる期待値とい
うものを高くすることを目標にプレーすることになりま
す。バックギャモンでは１ポイントあたり一定の価値が
あるという前提でアンリミットという条件でプレーする
ことが基本になっているため、それを前提に話を進めて
いきます。特に日本ではポイントマッチのほうがスタン
ダードになっていると思いますが、このゲームの長い歴
史の中で、ポイントマッチが行われるようになったのは
ごくごく最近、ここ数十年だと思います。
１ポイントあたり一定の価値というのは、たとえば、
１ポイント缶コーヒー１本おごるというようなもので、
１０本１回にもらってもあまり嬉しくないので、たとえ
ば５点負けたら５回おごってもらえるとかそういうふう
に考えてください。２倍勝てば２倍得するし、２倍負け
ると２倍損するということです。
そうなると、２点勝つことは１点勝つことの２倍の価
値があることがわかると思います。期待値を高めるには
単純に多くのゲームを勝つだけではなく、勝てるゲーム
での賭け点を大きくしたいのです。自分が有利なゲーム
であれば、ダブリングキューブを使うことにより賭け点
を２倍にしたいのです。もちろん、その１ゲームだけで
見れば、結果負けた時の負け点も２倍になりますが、長
い目で見れば得であるのでしたら、そうなった時も後悔
する必要は何もありません。これが一番重要な考え方だ
と思います。
本日の記事内でのポジションは、すべてアンリミット
セッションで、１点の価値は等価であり、ダブリングキ
ューブをつかうことも可能だと考えてください。
Pos 1
Money game
Blue on roll. Cube Action?| 2 |                 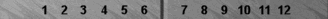| | 6 | GNUBg ID:AwAACAEAAAAAAA:cAkAAAAAAAAA
ダブリングキューブにからまない限りは具体的な勝率
は数字として出す必要はなく、比較候補の中でより優れ
ているものを選べればよかったのですが、ダブリングキ
ューブをつかうかどうかの判断では具体的な勝率という
ものが必要になります。
まず単純な例で、これがこのゲームでお互いにとって
最後のキューブアクションであるという例です。これは
相手がキューブを受ける（テイクする）という前提で、
キューブを打って賭け点を２倍にすることで期待値が２
倍になります。この２倍というのはマイナスも２倍にな
るので、もともとマイナス（不利）な局面で打つと損す
ることもご理解ください。
ギャモンの出目は前回述べたように２１種３６通りと
考えると、１８通りで互角、それよりも勝てる目が多け
れば有利、少なければ不利となります。これを感覚だけ
でプレーするのは危ないので、この３６通りはキューブ
判断の時は必ず数えましょう。
上にあげた図では２３通りであがることができて、
１３通りはあがることができません。あがれなければ白
の勝ちが確定なので、この局面は青が２３通り、白が
１３通りで勝つことができます。
青のこの時点（キューブ＝基本点が１点）での期待値
は（２３−１３）/３６で計算することができます。１０
通り分だけ有利ということです。なお、この計算で求め
られたものをmoney cubeless equitityと言って、上級者
たちが会話の中で局面の期待値を話している時にでてく
ることが多い数字です。
ここでは、この数字を具体的に計算する必要はありま
せん。有利であれば０より大きいということだけ理解い
ただければ十分です。
さて青がロール前にダブリングキューブをつかうこと
により、このゲームの賭け点が２倍になります。白がテ
イクするとして、さきほどの期待値が２倍になります。
もちろん、その後の青のロールで結果としてあがれれ
ば、キューブ打っておいたおかげで１点得した（＋１が
＋２になっているので）、あがれなければ逆に１点損し
たと明暗わかれるわけですが、期待値という考えでいけ
ばキューブ打っておいたほうがいいということはわかる
と思います。期待値ではパンは食べられないのだよとい
うのもわかるのですが、このような必勝が不可能なゲー
ムは期待値を最大にすべくプレーするのが戦略的に最善
（厳密にはリスク管理という大事な問題もあるのですが
、それはいずれ上級編があった時でいいでしょう、それ
は本当に難しい数学の話になりますので）と考えるしか
ないのです。
ところで、白が必ずテイクするという前提でしたが、
白はなんでも、勝つチャンスがある限りテイクすべきな
のでしょうか。
青側は有利であればダブルしていいというのはわかっ
たと思います。白がテイクしてもプラスな期待値が２倍
になるわけですし、パスならば手堅くキューブ打つ前の
基本点を確実に勝てるわけですから、いずれにしても得
なわけですから。
パスすれば全部負けだけど、テイクすれば勝つチャン
スも（ゼロな局面以外は）あるのだからテイクしたほう
が勝つチャンスは高いというのは事実です。問題は、賭
け点が２倍になるのを受け入れて割りに合うかというこ
とです。
パスすると１点負け、テイクして勝つと２点勝ち、テ
イクして負けると２点負けになります。パスした場合を
基準に考えると、テイクして勝てば３点得して、負ける
と１点損をします。得のほうが大きいので、少しくらい
不利ならばテイクしていいというのはわかると思います。
こういう時はこのように考えます。ゲインは３点、リス
クは１点なので、比率は3：1、それよりも勝つチャンス
があればテイクのほうが得と。ちょうど3：1になるとい
うのは、●●●：○と考えると、全体で４つのうち１つ
でいいということになります。これが２５％理論といわ
れているものの考え方です。
Pos 2
Money game
Blue on roll. Cube Action?| 2 | 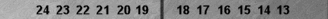  | | 6 | GNUBg ID:AwAAAAEAAAAAAA:cAkAAAAAAAAA
青は２７通りで上がれて大有利なので当然キューブ
を打ちます。白は青が上がれない９通りのみ勝つこと
ができます。これは全体で２５％ですね。
そのためこれはテイクしてもパスしても期待値は同
じです。
全体を３６通りで考えると
パスする ３６ゲームすべて１点負け −３６
テイクする ２７ゲームで２点負け −５４
９ゲームで２点勝ち ＋１８
合計 −３６
結論としては
青は５０％より勝率が高ければダブルすべきで、白
は２５％以上勝てるならばテイク、それ以下ならばパ
スでいいということになります。
初級者向けの話はここまででいいと思います。しか
し当日は参加者層が中級−オープン者が多かったので
より難しい話に発展していきます。
次回は、ラストロール以外でキューブを打つにはど
れくらいの勝率が必要なのかということを書きます。
来週中くらいには更新予定。たぶんあと２回。
|
|
|
No.3291
|
|
なまず２
nori
2012/01/19/17:52:49
No.3292
fairytails
2012/01/19/22:59:15
No.3294
ばるたん
2012/01/21/15:57:17
No.3295
ばるたん
2012/01/22/00:38:57
No.3297