| 125 |      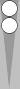 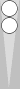   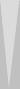              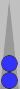   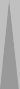        |
| 38 |
| 過去ログ[1] |
|---|
Money game
Blue on roll. Cube Action?125 38
[660へのレス] Re: Cube Action? 投稿者:もち 投稿日:2005/06/09(Thu) 21:14特殊ルールです。
Money Game, No jacoby , with beaver.
$1/pで$7がお互いの上限です。
つまり、このゲームで動くのは勝っても負けても7点までです。
[660へのレス] Re: Cube Action? 投稿者:daichan 投稿日:2005/06/10(Fri) 16:20too good
ちょっと怖いですが、与えたとして最高20ショットなので、トライします。
某帝国のルールに見えますが、それなら相手によってはキューブを打ち、引いてもらいます。
上限がわざわざ書いてあるのが気のなりますが・・・まさかギャモンプライスなくすためにビーバー?!
[660へのレス] Re: Cube Action? 投稿者:ふぃりあ 投稿日:2005/06/15(Wed) 15:12NoDouble Beaver
ここで青がキューブを打つとして、白はパスすると1点負けなので
勝率が50%より少し低いくらいでBeaver、Redoubleが成立しま
す。(Redoubleは、AnyMarketLoserで打ちます)
当たればほぼ勝ちのダブルショットが1回くらいと、さらにおまけ
のシングルショットくらいはもらえそうなので50%くらいはあり
そうです。
もし白側がBeaverが成立するほど高いのであれば、青側はギャモン
率の高さのみが現時点での期待値を高めているわけで、DMPになって
ギャモン勝ちが意味なくなるキューブは打てないでしょう。ダブルが
青の期待値を下げる、つまりTooGoodではなく、ダブルするにもたり
ない程度しかないNoDoubleな気がします。
7点ですので、8点ほぼフルに有効に近いので、ポイントマッチの
3Awaysよりも4Awaysに近いくらいでしょうかね。4Awaysであれ
ば、やはり青は勝率が50%よりも明らかに高くなければキューブ
は打てないわけで(白は41%あれば、パスするよりもテイクして
すぐリダブルするほうがましで、実際は最後の1枚ヒットするまで
チャンスがこなければリダブルしないわけで、単純に全部すぐリダ
ブルするよりも期待値が高いわけですから、五分五分程度でダブル
を打つのはあまりにありえなそうです)、単純にダブルするのにも
たりないのでしょう。
といっても実戦的には、相手が的確にBeaverするかわからないの
で、ダブル打つのもおもしろそうです。
以下の定理を証明しました。
--------------------------------------------------------
自分と相手のチェッカーが完全にすれ違ったものとする。
自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し、のこりの一枚が自分のアウターにあるものとする
。そのチェッカーのベアインまでの最短距離をm(1<=m<=6)
とし、この状態から一枚以上あげられる確率をP(n,m)とする。
また最後の2枚あがりで nポイントとmポイントに(1<=n,m<=6)
一枚ずつあるときに両方ともあがれる確率をB(n,m)とする。
このとき以下の等式が成り立つ。
P(n,m)=B(n,m)
--------------------------------------------------------
証明の詳細は書きませんが、上記条件を満たすときに一枚以上
あげられる出目の集合と2枚上がりできる出目の集合が同じ
になることを示せば十分です。
例を挙げて説明するとこの定理は以下のようなことを主張して
います。
position An=2
Money game
Blue on roll. Cube Action?2 70
m=4
position B
Match to 1, tied at 0
Blue on roll. Cube Action?2 6
position A でギャモンセーブできる確率はposition Bの勝率に等しい。
この定理を応用して以下のような問題を考えてみます。
Money game 4 81
A: 14/11, 3/2
B: 14/10
の比較になります。AもBも上記定理の条件を満たします。
次に自分の番が回ってきたときにAがギャモンセーブできる
確率は2と5に一枚ずつあるポジションで2枚ともあがれる
確率に等しく、Bがギャモンセーブできる確率は3と4に一枚
ずつ有るポジションで2枚ともあがれる確率に等しくなります。
2.5の法則(http://www.backgammon.gr.jp/links/kezuka/jp/research/last01.html)
を使うと2と5に一枚ずつあるポジションを選べば良いことがわ
かるのでAを選択すれば良いことがわかります。
[652へのレス] Re: 定理と応用 投稿者:もち 投稿日:2005/06/02(Thu) 10:01なるほど。
[652へのレス] Re: 定理と応用 投稿者:cameron 投稿日:2005/06/03(Fri) 22:50インナーが5pt6ptだと成立しないのですね。
これは実戦で使える方法で良いですね。
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 13:00さっき歩いているときに6ポイントに駒が無い場合について
の定理を思いつき証明しました。そのときは3ポイントにも
駒があることが必須になります。
上記定理の
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し」を
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=3)から5ポイントまでとぎれること無く連続して
分布し」に変更しても同様のことが言えます。
position C
Money game
Blue on roll. Cube Action?2 70
3から5まで連続して駒が分布しています。ベアインまでの最短距離が4ですからposition C でギャモンセーブできる確率はposition Dの勝率に等しくなります。
position D
Match to 1, tied at 0
Blue on roll. Cube Action?2 7
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 15:38さらにこれは等式が成り立つということを主張するのではなく、
ギャモンセーブの1のチョイスの問題で2.5の法則により正解を選べるという主張をするのであれば、次のことが言える。
自分の14枚のチェッカーが4ポイントと5ポイントを含んで連続してインナーに分布し、チェッカーがあるポイントの中で最小のポイントnに複数枚チェッカーがあるとする。のこりの一枚がアウターにあり、ベアインまでの距離をm(1<=m<=6)とする。
このとき 出目1でm+6/m+5 とするか n/n-1とするかの選択が
あるとき (n,m-1) と(n-1,m)に2.5の法則を適用すれば
正解が選択できる。
証明の概略
上の二つの定理から4ポイント、5ポイントにチェッカーが14枚あり、4ポイントには複数枚有る場合のみを考えれば良い。このときm=1,2,3,4,5,6で2.5の法則により選んだムーブがギャモンセーブの1のチョイスの問題で正解となっていることを確かめれば良い。
Money game
Blue on roll. Cube Action?125 38
[660へのレス] Re: Cube Action? 投稿者:もち 投稿日:2005/06/09(Thu) 21:14特殊ルールです。
Money Game, No jacoby , with beaver.
$1/pで$7がお互いの上限です。
つまり、このゲームで動くのは勝っても負けても7点までです。
[660へのレス] Re: Cube Action? 投稿者:daichan 投稿日:2005/06/10(Fri) 16:20too good
ちょっと怖いですが、与えたとして最高20ショットなので、トライします。
某帝国のルールに見えますが、それなら相手によってはキューブを打ち、引いてもらいます。
上限がわざわざ書いてあるのが気のなりますが・・・まさかギャモンプライスなくすためにビーバー?!
[660へのレス] Re: Cube Action? 投稿者:ふぃりあ 投稿日:2005/06/15(Wed) 15:12NoDouble Beaver
ここで青がキューブを打つとして、白はパスすると1点負けなので
勝率が50%より少し低いくらいでBeaver、Redoubleが成立しま
す。(Redoubleは、AnyMarketLoserで打ちます)
当たればほぼ勝ちのダブルショットが1回くらいと、さらにおまけ
のシングルショットくらいはもらえそうなので50%くらいはあり
そうです。
もし白側がBeaverが成立するほど高いのであれば、青側はギャモン
率の高さのみが現時点での期待値を高めているわけで、DMPになって
ギャモン勝ちが意味なくなるキューブは打てないでしょう。ダブルが
青の期待値を下げる、つまりTooGoodではなく、ダブルするにもたり
ない程度しかないNoDoubleな気がします。
7点ですので、8点ほぼフルに有効に近いので、ポイントマッチの
3Awaysよりも4Awaysに近いくらいでしょうかね。4Awaysであれ
ば、やはり青は勝率が50%よりも明らかに高くなければキューブ
は打てないわけで(白は41%あれば、パスするよりもテイクして
すぐリダブルするほうがましで、実際は最後の1枚ヒットするまで
チャンスがこなければリダブルしないわけで、単純に全部すぐリダ
ブルするよりも期待値が高いわけですから、五分五分程度でダブル
を打つのはあまりにありえなそうです)、単純にダブルするのにも
たりないのでしょう。
といっても実戦的には、相手が的確にBeaverするかわからないの
で、ダブル打つのもおもしろそうです。
以下の定理を証明しました。
--------------------------------------------------------
自分と相手のチェッカーが完全にすれ違ったものとする。
自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し、のこりの一枚が自分のアウターにあるものとする
。そのチェッカーのベアインまでの最短距離をm(1<=m<=6)
とし、この状態から一枚以上あげられる確率をP(n,m)とする。
また最後の2枚あがりで nポイントとmポイントに(1<=n,m<=6)
一枚ずつあるときに両方ともあがれる確率をB(n,m)とする。
このとき以下の等式が成り立つ。
P(n,m)=B(n,m)
--------------------------------------------------------
証明の詳細は書きませんが、上記条件を満たすときに一枚以上
あげられる出目の集合と2枚上がりできる出目の集合が同じ
になることを示せば十分です。
例を挙げて説明するとこの定理は以下のようなことを主張して
います。
position An=2
Money game
Blue on roll. Cube Action?2 70
m=4
position B
Match to 1, tied at 0
Blue on roll. Cube Action?2 6
position A でギャモンセーブできる確率はposition Bの勝率に等しい。
この定理を応用して以下のような問題を考えてみます。
Money game 4 81
A: 14/11, 3/2
B: 14/10
の比較になります。AもBも上記定理の条件を満たします。
次に自分の番が回ってきたときにAがギャモンセーブできる
確率は2と5に一枚ずつあるポジションで2枚ともあがれる
確率に等しく、Bがギャモンセーブできる確率は3と4に一枚
ずつ有るポジションで2枚ともあがれる確率に等しくなります。
2.5の法則(http://www.backgammon.gr.jp/links/kezuka/jp/research/last01.html)
を使うと2と5に一枚ずつあるポジションを選べば良いことがわ
かるのでAを選択すれば良いことがわかります。
[652へのレス] Re: 定理と応用 投稿者:もち 投稿日:2005/06/02(Thu) 10:01なるほど。
[652へのレス] Re: 定理と応用 投稿者:cameron 投稿日:2005/06/03(Fri) 22:50インナーが5pt6ptだと成立しないのですね。
これは実戦で使える方法で良いですね。
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 13:00さっき歩いているときに6ポイントに駒が無い場合について
の定理を思いつき証明しました。そのときは3ポイントにも
駒があることが必須になります。
上記定理の
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し」を
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=3)から5ポイントまでとぎれること無く連続して
分布し」に変更しても同様のことが言えます。
position C
Money game
Blue on roll. Cube Action?2 70
3から5まで連続して駒が分布しています。ベアインまでの最短距離が4ですからposition C でギャモンセーブできる確率はposition Dの勝率に等しくなります。
position D
Match to 1, tied at 0
Blue on roll. Cube Action?2 7
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 15:38さらにこれは等式が成り立つということを主張するのではなく、
ギャモンセーブの1のチョイスの問題で2.5の法則により正解を選べるという主張をするのであれば、次のことが言える。
自分の14枚のチェッカーが4ポイントと5ポイントを含んで連続してインナーに分布し、チェッカーがあるポイントの中で最小のポイントnに複数枚チェッカーがあるとする。のこりの一枚がアウターにあり、ベアインまでの距離をm(1<=m<=6)とする。
このとき 出目1でm+6/m+5 とするか n/n-1とするかの選択が
あるとき (n,m-1) と(n-1,m)に2.5の法則を適用すれば
正解が選択できる。
証明の概略
上の二つの定理から4ポイント、5ポイントにチェッカーが14枚あり、4ポイントには複数枚有る場合のみを考えれば良い。このときm=1,2,3,4,5,6で2.5の法則により選んだムーブがギャモンセーブの1のチョイスの問題で正解となっていることを確かめれば良い。
Money game
Blue on roll. Cube Action?125 38
[660へのレス] Re: Cube Action? 投稿者:もち 投稿日:2005/06/09(Thu) 21:14特殊ルールです。
Money Game, No jacoby , with beaver.
$1/pで$7がお互いの上限です。
つまり、このゲームで動くのは勝っても負けても7点までです。
[660へのレス] Re: Cube Action? 投稿者:daichan 投稿日:2005/06/10(Fri) 16:20too good
ちょっと怖いですが、与えたとして最高20ショットなので、トライします。
某帝国のルールに見えますが、それなら相手によってはキューブを打ち、引いてもらいます。
上限がわざわざ書いてあるのが気のなりますが・・・まさかギャモンプライスなくすためにビーバー?!
[660へのレス] Re: Cube Action? 投稿者:ふぃりあ 投稿日:2005/06/15(Wed) 15:12NoDouble Beaver
ここで青がキューブを打つとして、白はパスすると1点負けなので
勝率が50%より少し低いくらいでBeaver、Redoubleが成立しま
す。(Redoubleは、AnyMarketLoserで打ちます)
当たればほぼ勝ちのダブルショットが1回くらいと、さらにおまけ
のシングルショットくらいはもらえそうなので50%くらいはあり
そうです。
もし白側がBeaverが成立するほど高いのであれば、青側はギャモン
率の高さのみが現時点での期待値を高めているわけで、DMPになって
ギャモン勝ちが意味なくなるキューブは打てないでしょう。ダブルが
青の期待値を下げる、つまりTooGoodではなく、ダブルするにもたり
ない程度しかないNoDoubleな気がします。
7点ですので、8点ほぼフルに有効に近いので、ポイントマッチの
3Awaysよりも4Awaysに近いくらいでしょうかね。4Awaysであれ
ば、やはり青は勝率が50%よりも明らかに高くなければキューブ
は打てないわけで(白は41%あれば、パスするよりもテイクして
すぐリダブルするほうがましで、実際は最後の1枚ヒットするまで
チャンスがこなければリダブルしないわけで、単純に全部すぐリダ
ブルするよりも期待値が高いわけですから、五分五分程度でダブル
を打つのはあまりにありえなそうです)、単純にダブルするのにも
たりないのでしょう。
といっても実戦的には、相手が的確にBeaverするかわからないの
で、ダブル打つのもおもしろそうです。
以下の定理を証明しました。
--------------------------------------------------------
自分と相手のチェッカーが完全にすれ違ったものとする。
自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し、のこりの一枚が自分のアウターにあるものとする
。そのチェッカーのベアインまでの最短距離をm(1<=m<=6)
とし、この状態から一枚以上あげられる確率をP(n,m)とする。
また最後の2枚あがりで nポイントとmポイントに(1<=n,m<=6)
一枚ずつあるときに両方ともあがれる確率をB(n,m)とする。
このとき以下の等式が成り立つ。
P(n,m)=B(n,m)
--------------------------------------------------------
証明の詳細は書きませんが、上記条件を満たすときに一枚以上
あげられる出目の集合と2枚上がりできる出目の集合が同じ
になることを示せば十分です。
例を挙げて説明するとこの定理は以下のようなことを主張して
います。
position An=2
Money game
Blue on roll. Cube Action?2 70
m=4
position B
Match to 1, tied at 0
Blue on roll. Cube Action?2 6
position A でギャモンセーブできる確率はposition Bの勝率に等しい。
この定理を応用して以下のような問題を考えてみます。
Money game 4 81
A: 14/11, 3/2
B: 14/10
の比較になります。AもBも上記定理の条件を満たします。
次に自分の番が回ってきたときにAがギャモンセーブできる
確率は2と5に一枚ずつあるポジションで2枚ともあがれる
確率に等しく、Bがギャモンセーブできる確率は3と4に一枚
ずつ有るポジションで2枚ともあがれる確率に等しくなります。
2.5の法則(http://www.backgammon.gr.jp/links/kezuka/jp/research/last01.html)
を使うと2と5に一枚ずつあるポジションを選べば良いことがわ
かるのでAを選択すれば良いことがわかります。
[652へのレス] Re: 定理と応用 投稿者:もち 投稿日:2005/06/02(Thu) 10:01なるほど。
[652へのレス] Re: 定理と応用 投稿者:cameron 投稿日:2005/06/03(Fri) 22:50インナーが5pt6ptだと成立しないのですね。
これは実戦で使える方法で良いですね。
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 13:00さっき歩いているときに6ポイントに駒が無い場合について
の定理を思いつき証明しました。そのときは3ポイントにも
駒があることが必須になります。
上記定理の
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し」を
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=3)から5ポイントまでとぎれること無く連続して
分布し」に変更しても同様のことが言えます。
position C
Money game
Blue on roll. Cube Action?2 70
3から5まで連続して駒が分布しています。ベアインまでの最短距離が4ですからposition C でギャモンセーブできる確率はposition Dの勝率に等しくなります。
position D
Match to 1, tied at 0
Blue on roll. Cube Action?2 7
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 15:38さらにこれは等式が成り立つということを主張するのではなく、
ギャモンセーブの1のチョイスの問題で2.5の法則により正解を選べるという主張をするのであれば、次のことが言える。
自分の14枚のチェッカーが4ポイントと5ポイントを含んで連続してインナーに分布し、チェッカーがあるポイントの中で最小のポイントnに複数枚チェッカーがあるとする。のこりの一枚がアウターにあり、ベアインまでの距離をm(1<=m<=6)とする。
このとき 出目1でm+6/m+5 とするか n/n-1とするかの選択が
あるとき (n,m-1) と(n-1,m)に2.5の法則を適用すれば
正解が選択できる。
証明の概略
上の二つの定理から4ポイント、5ポイントにチェッカーが14枚あり、4ポイントには複数枚有る場合のみを考えれば良い。このときm=1,2,3,4,5,6で2.5の法則により選んだムーブがギャモンセーブの1のチョイスの問題で正解となっていることを確かめれば良い。
Money game
Blue on roll. Cube Action?125 38
[660へのレス] Re: Cube Action? 投稿者:もち 投稿日:2005/06/09(Thu) 21:14特殊ルールです。
Money Game, No jacoby , with beaver.
$1/pで$7がお互いの上限です。
つまり、このゲームで動くのは勝っても負けても7点までです。
[660へのレス] Re: Cube Action? 投稿者:daichan 投稿日:2005/06/10(Fri) 16:20too good
ちょっと怖いですが、与えたとして最高20ショットなので、トライします。
某帝国のルールに見えますが、それなら相手によってはキューブを打ち、引いてもらいます。
上限がわざわざ書いてあるのが気のなりますが・・・まさかギャモンプライスなくすためにビーバー?!
[660へのレス] Re: Cube Action? 投稿者:ふぃりあ 投稿日:2005/06/15(Wed) 15:12NoDouble Beaver
ここで青がキューブを打つとして、白はパスすると1点負けなので
勝率が50%より少し低いくらいでBeaver、Redoubleが成立しま
す。(Redoubleは、AnyMarketLoserで打ちます)
当たればほぼ勝ちのダブルショットが1回くらいと、さらにおまけ
のシングルショットくらいはもらえそうなので50%くらいはあり
そうです。
もし白側がBeaverが成立するほど高いのであれば、青側はギャモン
率の高さのみが現時点での期待値を高めているわけで、DMPになって
ギャモン勝ちが意味なくなるキューブは打てないでしょう。ダブルが
青の期待値を下げる、つまりTooGoodではなく、ダブルするにもたり
ない程度しかないNoDoubleな気がします。
7点ですので、8点ほぼフルに有効に近いので、ポイントマッチの
3Awaysよりも4Awaysに近いくらいでしょうかね。4Awaysであれ
ば、やはり青は勝率が50%よりも明らかに高くなければキューブ
は打てないわけで(白は41%あれば、パスするよりもテイクして
すぐリダブルするほうがましで、実際は最後の1枚ヒットするまで
チャンスがこなければリダブルしないわけで、単純に全部すぐリダ
ブルするよりも期待値が高いわけですから、五分五分程度でダブル
を打つのはあまりにありえなそうです)、単純にダブルするのにも
たりないのでしょう。
といっても実戦的には、相手が的確にBeaverするかわからないの
で、ダブル打つのもおもしろそうです。
以下の定理を証明しました。
--------------------------------------------------------
自分と相手のチェッカーが完全にすれ違ったものとする。
自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し、のこりの一枚が自分のアウターにあるものとする
。そのチェッカーのベアインまでの最短距離をm(1<=m<=6)
とし、この状態から一枚以上あげられる確率をP(n,m)とする。
また最後の2枚あがりで nポイントとmポイントに(1<=n,m<=6)
一枚ずつあるときに両方ともあがれる確率をB(n,m)とする。
このとき以下の等式が成り立つ。
P(n,m)=B(n,m)
--------------------------------------------------------
証明の詳細は書きませんが、上記条件を満たすときに一枚以上
あげられる出目の集合と2枚上がりできる出目の集合が同じ
になることを示せば十分です。
例を挙げて説明するとこの定理は以下のようなことを主張して
います。
position An=2
Money game
Blue on roll. Cube Action?2 70
m=4
position B
Match to 1, tied at 0
Blue on roll. Cube Action?2 6
position A でギャモンセーブできる確率はposition Bの勝率に等しい。
この定理を応用して以下のような問題を考えてみます。
Money game 4 81
A: 14/11, 3/2
B: 14/10
の比較になります。AもBも上記定理の条件を満たします。
次に自分の番が回ってきたときにAがギャモンセーブできる
確率は2と5に一枚ずつあるポジションで2枚ともあがれる
確率に等しく、Bがギャモンセーブできる確率は3と4に一枚
ずつ有るポジションで2枚ともあがれる確率に等しくなります。
2.5の法則(http://www.backgammon.gr.jp/links/kezuka/jp/research/last01.html)
を使うと2と5に一枚ずつあるポジションを選べば良いことがわ
かるのでAを選択すれば良いことがわかります。
[652へのレス] Re: 定理と応用 投稿者:もち 投稿日:2005/06/02(Thu) 10:01なるほど。
[652へのレス] Re: 定理と応用 投稿者:cameron 投稿日:2005/06/03(Fri) 22:50インナーが5pt6ptだと成立しないのですね。
これは実戦で使える方法で良いですね。
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 13:00さっき歩いているときに6ポイントに駒が無い場合について
の定理を思いつき証明しました。そのときは3ポイントにも
駒があることが必須になります。
上記定理の
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し」を
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=3)から5ポイントまでとぎれること無く連続して
分布し」に変更しても同様のことが言えます。
position C
Money game
Blue on roll. Cube Action?2 70
3から5まで連続して駒が分布しています。ベアインまでの最短距離が4ですからposition C でギャモンセーブできる確率はposition Dの勝率に等しくなります。
position D
Match to 1, tied at 0
Blue on roll. Cube Action?2 7
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 15:38さらにこれは等式が成り立つということを主張するのではなく、
ギャモンセーブの1のチョイスの問題で2.5の法則により正解を選べるという主張をするのであれば、次のことが言える。
自分の14枚のチェッカーが4ポイントと5ポイントを含んで連続してインナーに分布し、チェッカーがあるポイントの中で最小のポイントnに複数枚チェッカーがあるとする。のこりの一枚がアウターにあり、ベアインまでの距離をm(1<=m<=6)とする。
このとき 出目1でm+6/m+5 とするか n/n-1とするかの選択が
あるとき (n,m-1) と(n-1,m)に2.5の法則を適用すれば
正解が選択できる。
証明の概略
上の二つの定理から4ポイント、5ポイントにチェッカーが14枚あり、4ポイントには複数枚有る場合のみを考えれば良い。このときm=1,2,3,4,5,6で2.5の法則により選んだムーブがギャモンセーブの1のチョイスの問題で正解となっていることを確かめれば良い。
Money game
Blue on roll. Cube Action?125 38
[660へのレス] Re: Cube Action? 投稿者:もち 投稿日:2005/06/09(Thu) 21:14特殊ルールです。
Money Game, No jacoby , with beaver.
$1/pで$7がお互いの上限です。
つまり、このゲームで動くのは勝っても負けても7点までです。
[660へのレス] Re: Cube Action? 投稿者:daichan 投稿日:2005/06/10(Fri) 16:20too good
ちょっと怖いですが、与えたとして最高20ショットなので、トライします。
某帝国のルールに見えますが、それなら相手によってはキューブを打ち、引いてもらいます。
上限がわざわざ書いてあるのが気のなりますが・・・まさかギャモンプライスなくすためにビーバー?!
[660へのレス] Re: Cube Action? 投稿者:ふぃりあ 投稿日:2005/06/15(Wed) 15:12NoDouble Beaver
ここで青がキューブを打つとして、白はパスすると1点負けなので
勝率が50%より少し低いくらいでBeaver、Redoubleが成立しま
す。(Redoubleは、AnyMarketLoserで打ちます)
当たればほぼ勝ちのダブルショットが1回くらいと、さらにおまけ
のシングルショットくらいはもらえそうなので50%くらいはあり
そうです。
もし白側がBeaverが成立するほど高いのであれば、青側はギャモン
率の高さのみが現時点での期待値を高めているわけで、DMPになって
ギャモン勝ちが意味なくなるキューブは打てないでしょう。ダブルが
青の期待値を下げる、つまりTooGoodではなく、ダブルするにもたり
ない程度しかないNoDoubleな気がします。
7点ですので、8点ほぼフルに有効に近いので、ポイントマッチの
3Awaysよりも4Awaysに近いくらいでしょうかね。4Awaysであれ
ば、やはり青は勝率が50%よりも明らかに高くなければキューブ
は打てないわけで(白は41%あれば、パスするよりもテイクして
すぐリダブルするほうがましで、実際は最後の1枚ヒットするまで
チャンスがこなければリダブルしないわけで、単純に全部すぐリダ
ブルするよりも期待値が高いわけですから、五分五分程度でダブル
を打つのはあまりにありえなそうです)、単純にダブルするのにも
たりないのでしょう。
といっても実戦的には、相手が的確にBeaverするかわからないの
で、ダブル打つのもおもしろそうです。
以下の定理を証明しました。
--------------------------------------------------------
自分と相手のチェッカーが完全にすれ違ったものとする。
自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し、のこりの一枚が自分のアウターにあるものとする
。そのチェッカーのベアインまでの最短距離をm(1<=m<=6)
とし、この状態から一枚以上あげられる確率をP(n,m)とする。
また最後の2枚あがりで nポイントとmポイントに(1<=n,m<=6)
一枚ずつあるときに両方ともあがれる確率をB(n,m)とする。
このとき以下の等式が成り立つ。
P(n,m)=B(n,m)
--------------------------------------------------------
証明の詳細は書きませんが、上記条件を満たすときに一枚以上
あげられる出目の集合と2枚上がりできる出目の集合が同じ
になることを示せば十分です。
例を挙げて説明するとこの定理は以下のようなことを主張して
います。
position An=2
Money game
Blue on roll. Cube Action?2 70
m=4
position B
Match to 1, tied at 0
Blue on roll. Cube Action?2 6
position A でギャモンセーブできる確率はposition Bの勝率に等しい。
この定理を応用して以下のような問題を考えてみます。
Money game 4 81
A: 14/11, 3/2
B: 14/10
の比較になります。AもBも上記定理の条件を満たします。
次に自分の番が回ってきたときにAがギャモンセーブできる
確率は2と5に一枚ずつあるポジションで2枚ともあがれる
確率に等しく、Bがギャモンセーブできる確率は3と4に一枚
ずつ有るポジションで2枚ともあがれる確率に等しくなります。
2.5の法則(http://www.backgammon.gr.jp/links/kezuka/jp/research/last01.html)
を使うと2と5に一枚ずつあるポジションを選べば良いことがわ
かるのでAを選択すれば良いことがわかります。
[652へのレス] Re: 定理と応用 投稿者:もち 投稿日:2005/06/02(Thu) 10:01なるほど。
[652へのレス] Re: 定理と応用 投稿者:cameron 投稿日:2005/06/03(Fri) 22:50インナーが5pt6ptだと成立しないのですね。
これは実戦で使える方法で良いですね。
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 13:00さっき歩いているときに6ポイントに駒が無い場合について
の定理を思いつき証明しました。そのときは3ポイントにも
駒があることが必須になります。
上記定理の
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=4)から6ポイントまでとぎれること無く連続して
分布し」を
「自分の14枚のチェッカーが自分のインナーのnポイント
(1<=n<=3)から5ポイントまでとぎれること無く連続して
分布し」に変更しても同様のことが言えます。
position C
Money game
Blue on roll. Cube Action?2 70
3から5まで連続して駒が分布しています。ベアインまでの最短距離が4ですからposition C でギャモンセーブできる確率はposition Dの勝率に等しくなります。
position D
Match to 1, tied at 0
Blue on roll. Cube Action?2 7
[652へのレス] Re: 定理と応用 投稿者:itikawa 投稿日:2005/06/07(Tue) 15:38さらにこれは等式が成り立つということを主張するのではなく、
ギャモンセーブの1のチョイスの問題で2.5の法則により正解を選べるという主張をするのであれば、次のことが言える。
自分の14枚のチェッカーが4ポイントと5ポイントを含んで連続してインナーに分布し、チェッカーがあるポイントの中で最小のポイントnに複数枚チェッカーがあるとする。のこりの一枚がアウターにあり、ベアインまでの距離をm(1<=m<=6)とする。
このとき 出目1でm+6/m+5 とするか n/n-1とするかの選択が
あるとき (n,m-1) と(n-1,m)に2.5の法則を適用すれば
正解が選択できる。
証明の概略
上の二つの定理から4ポイント、5ポイントにチェッカーが14枚あり、4ポイントには複数枚有る場合のみを考えれば良い。このときm=1,2,3,4,5,6で2.5の法則により選んだムーブがギャモンセーブの1のチョイスの問題で正解となっていることを確かめれば良い。